Theory

This general workflow followed by the code can be summarized as:

Code workflow

We now detail what each of the steps given in the flowchart signify and add important details on how it is implemented.

Construction of STGB microstate

Each bicrystal containing the required symmetric tilt grain boundary is constructed by:

1. Creating an interpenetrating lattice by combining two lattices, one rotated by \(\theta/2\) andthe other by \(-\theta/2\), where \(\theta\) is the misorientation angle.

2. Selecting a gb location (with a parameter gb_position used in src.GBKineticsRunController.runGBkinetics()) and deleting atoms of grain 1 from one side of the gb position and from grain 2 on the other side.

This results in creation of a bicrystal as shown below:

\(\Sigma\) 17 [001](410) symmetric tilt grain boundary as-cut configuration

The bicrystal thus created is not typically in the ground state. To arrive at the ground state, we use the γ-surface method, wherein the two grains are displaced relative to each other in the GB plane and energy is minimized (carried out by running gridSearch). This results in creation of bicrystal with GB in its ground state, as shown below:

STGB in ground state

The relative displacement that results in the lowest post-minimized energy is recorded, as it serves as input to the latter part of the workflow.

Enumeration of disconnection modes

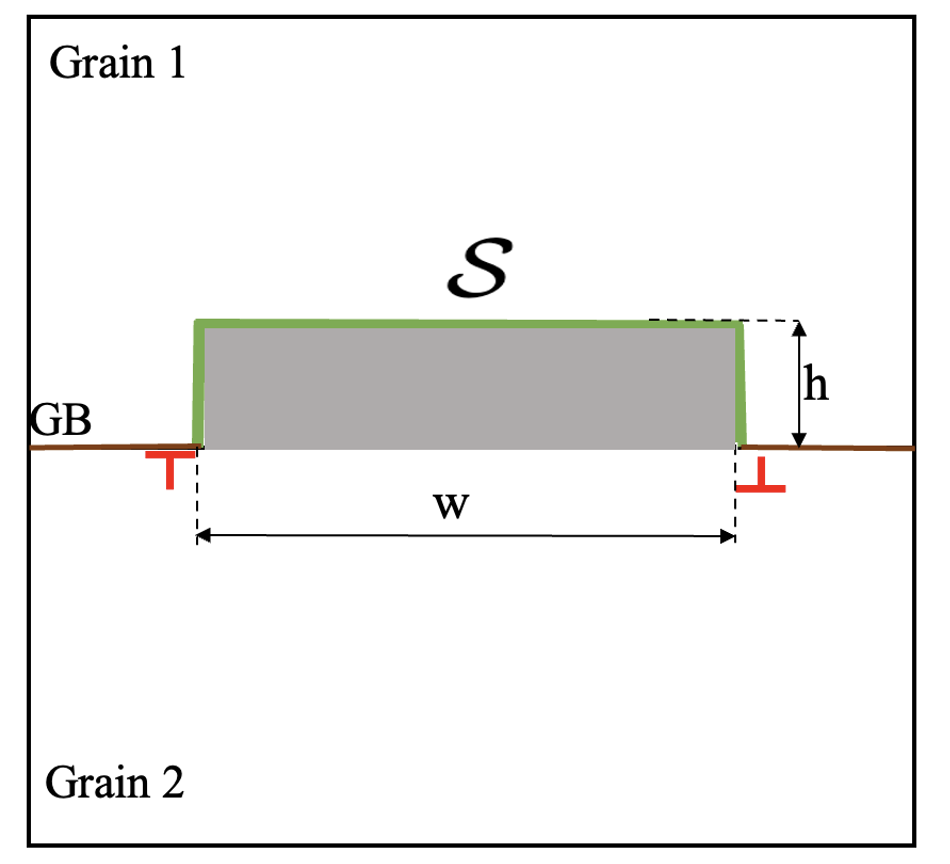
We use Smith normal norm (SNF) bicrystallography to enumerate the disconnection modes (b, h) of the STGB, where b and h denote the disconnection’s Burgers vector and step height, respectively. SNF bicrystallography is a powerful framework based on integer matrix algebra to automate the generation of rational GBs, and enumerate disconnection modes in GBs. For further details on SNF bicrystallography, we refer the reader to Admal et al.[1] (https://doi.org/10.1016/j.actamat.2022.118340).

Construction of atomistic GB migration images

We assume that GB migrates due to nucleation and migration of disconnections along the GB. A pictorial representation of such a migration is shown below:

Pictorial representation of GB migration due to disconnection nucleation and glide

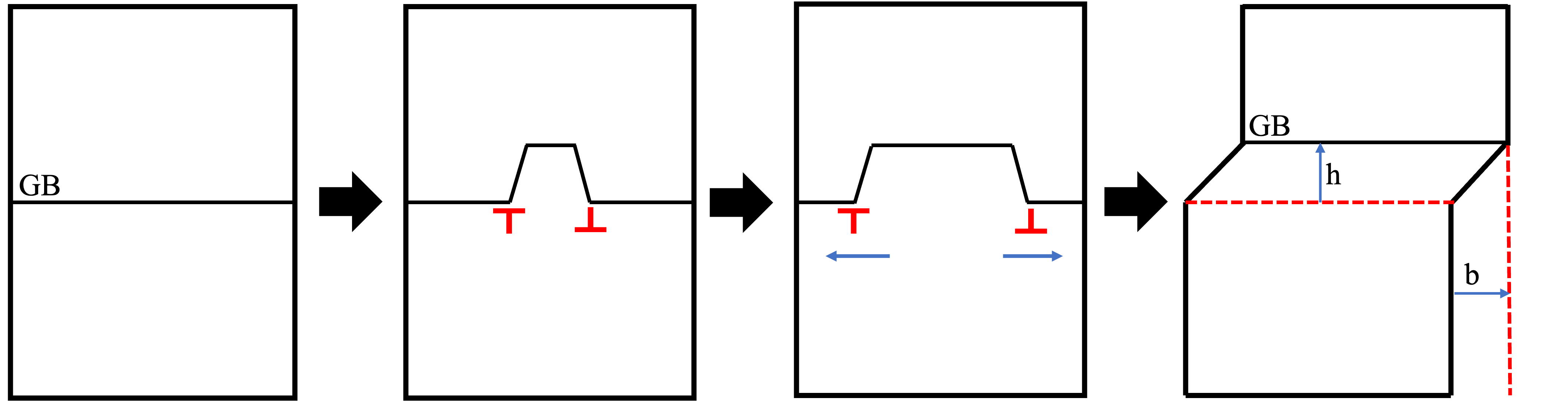
To construct a bicrystal with a disconnection step, we follow the following procedure:

1. Create an interpenetrating lattice by combining two lattices, one rotated by \(\theta/2\) and the other by \(-\theta/2\)

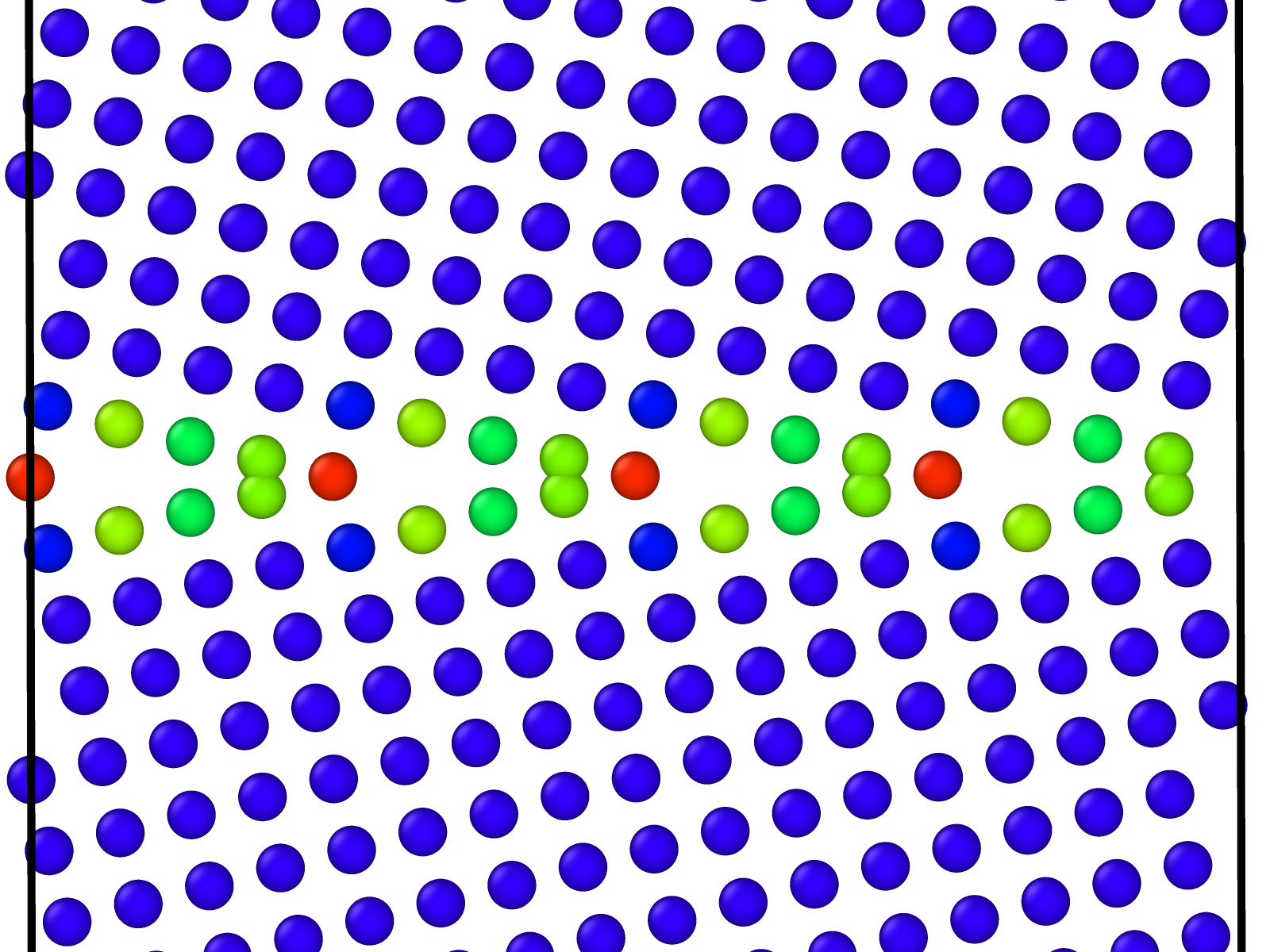
2. To generate a disconnection of burgers vector b, step height h and width w (as shown in the figure below), we displace all atoms in the dichromatic pattern according to the plastic displacement field:

\[u(\boldsymbol{x};\mathcal S) = -\frac{\boldsymbol{b}\Omega(\boldsymbol{x};\mathcal S)}{4\pi}\]

where \(\Omega(\boldsymbol{x})\) is the solid angle subtended by the dislocation dipole on a particle at position \(\boldsymbol{x}\).

Pictorial representation of a GB with disconnection on it

3. Next, a stepped GB is formed by deleting respective atoms on either side of GB, as shown in step 2 of figure above.

This results in creation of atomic configuration of a bicrystal with a disconnection inserted in it. The displacement jump at the GB can be readily observed in the following figure:

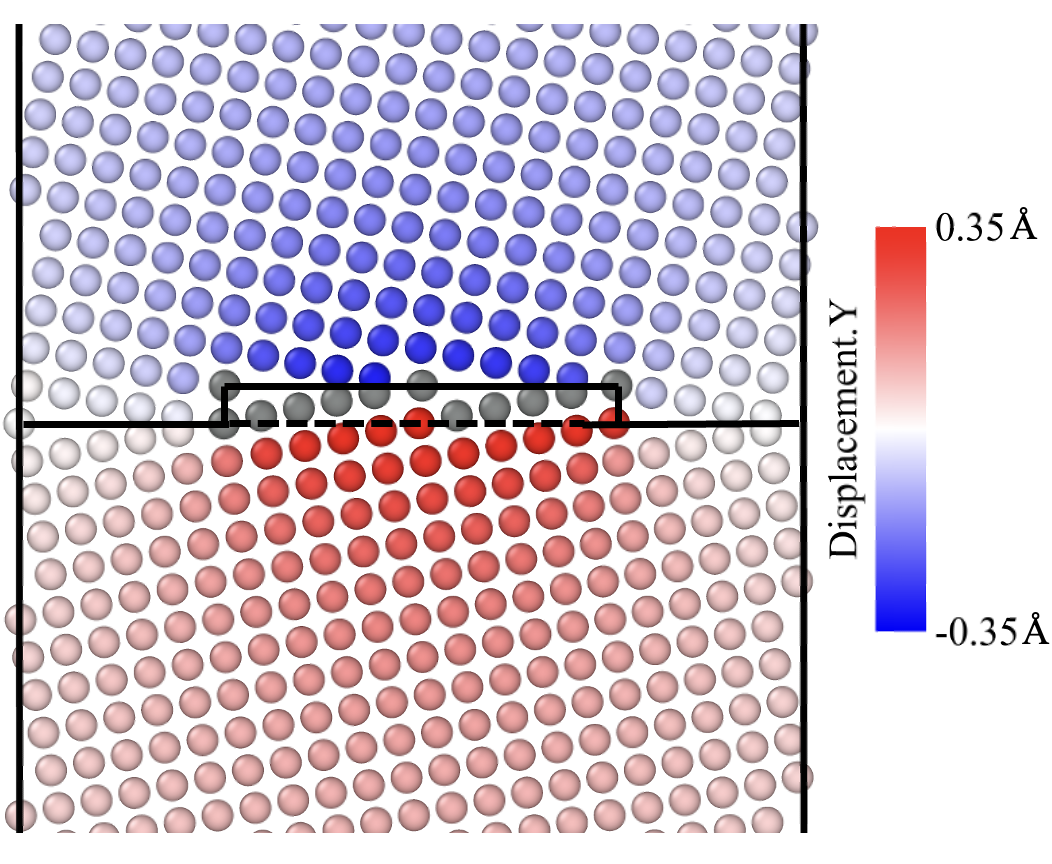
Atomic configuration after insertion of a disconnection

4. The atomix configuration created in not at ground state. To get to the ground state energy structure, we minimize the structure using LAMMPS and get the actual GB microstate with disconnection inserted.

Running Step 1-4 such that disconnection glides through the whole GB provides us the atomic configurations we are after, shown in the figures below:

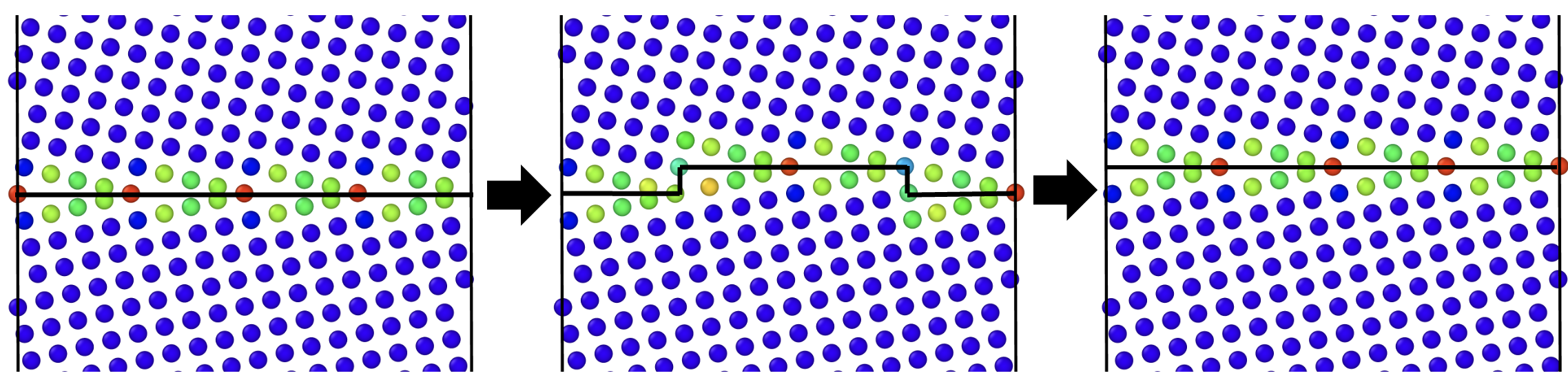
Atomic configurations generated, showing GB migration based on disconnection nucleation and glide.

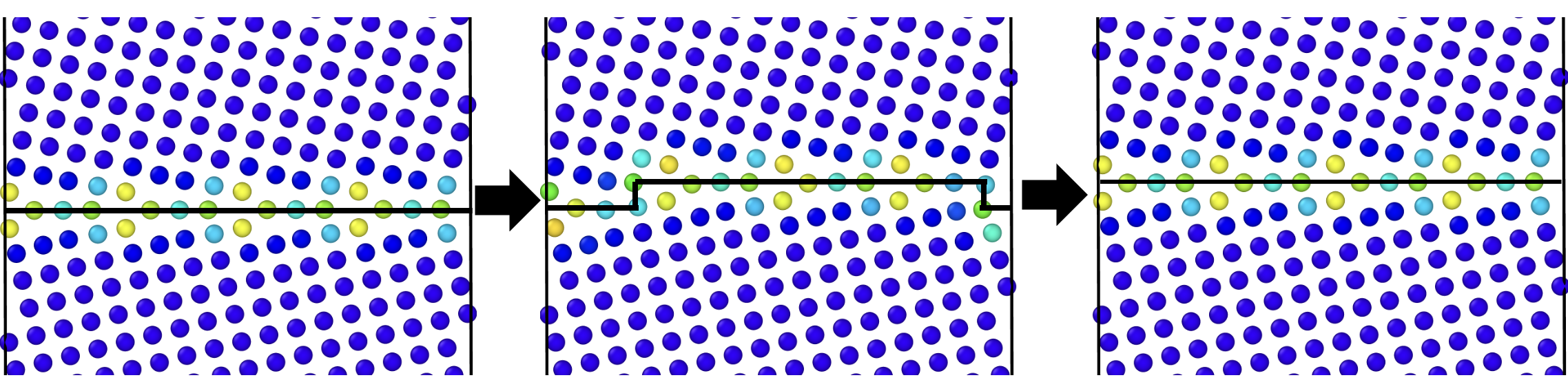
Final (minimized) atomic configurations generated, showing GB migration based on disconnection nucleation and glide.

Mapping the atomic shuffles

We now compute the shuffle maps for the atoms that have transformed from one grain to another during disconnection nucleation and glide. Such maps serve as intermediate images for NEB calculation in the next step. Shuffle maps are calculated using the optimal transport method developed by Chesser et al. [2,3]. The chosen shuffle map, the min-shuffle map, minimizes net shuffle distance in the dichromatic pattern. By increasing the regularization parameter, it is possible to select for mappings with larger net displacements such as those observed at high temperatures in specific GBs.

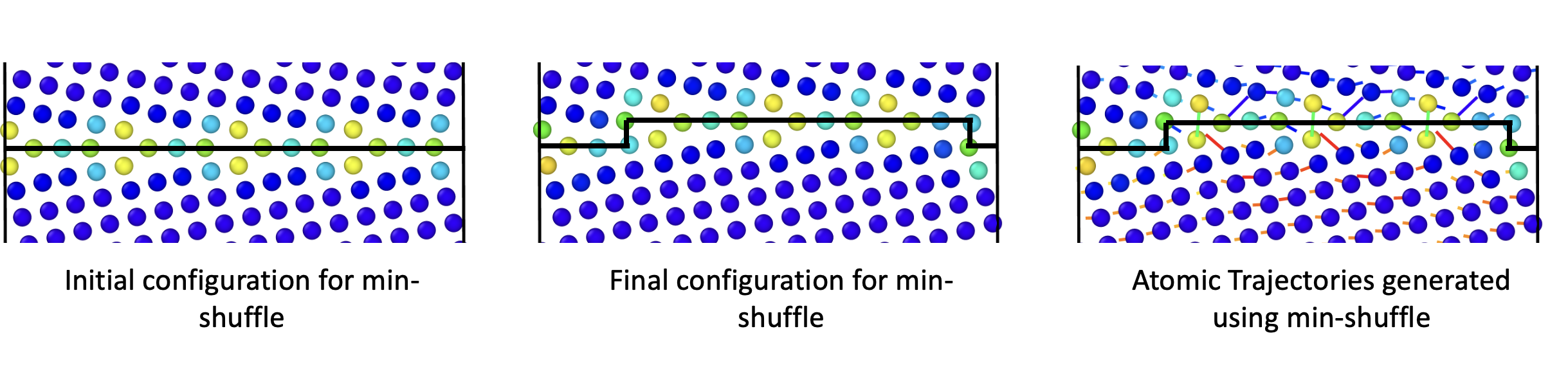
Atomic configurations used as input for min-shuffle algorithm and final trajectories generated.

Evaluation of the energy barrier and trajectories

We employ climbing image NEB method [4] to calculate the minimum energy paths (MEPs), i.e. plots of energy versus the reaction coordinate (width or the normalized width of the disconnection dipole), of disconnection modes in the absence of external loads. The NEB is implemented using the LAMMPS neb module with nudging forces parallel and perpendicular to the configurational path with a unitary spring constant.

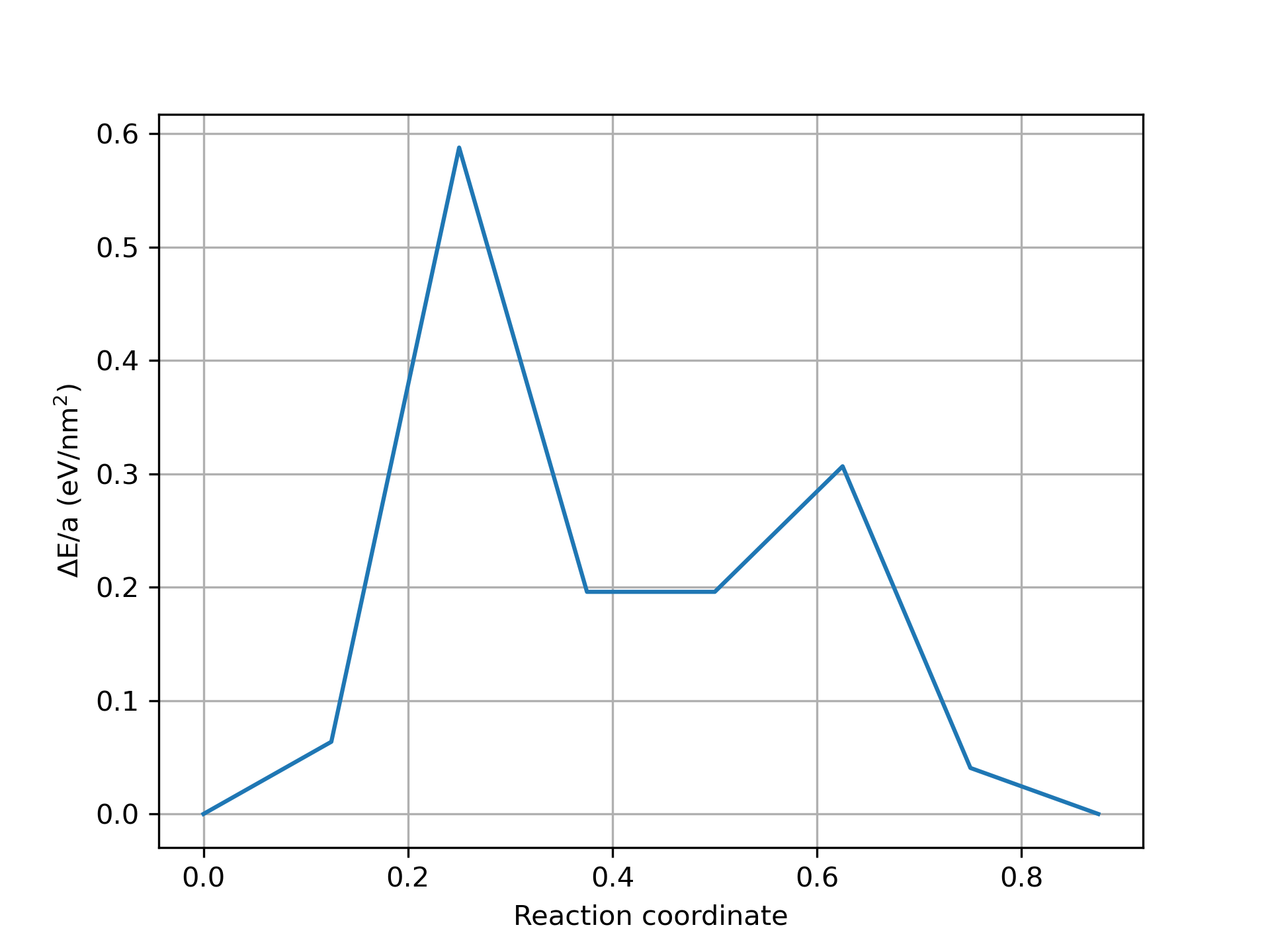
MEP generated using NEB calculations using 4 intermediate images

References

[1] N. C. Admal, T. Ahmed, E. Martinez, G. Po, Interface dislocations and grain boundary disconnections using smith normal bicrystallography, Acta Materialia 240 (2022)118340.

[2] I. Chesser, B. Runnels, E. Holm, A taxonomy of grain boundary migration mechanisms via displacement texture characterization, Acta Materialia 222 (2022) 117425.

[3] I. Chesser, E. Holm, B. Runnels, Optimal transportation of grain boundaries: A forward model for predicting migration mechanisms, Acta Materialia 210 (2021) 116823.

[4] G. Henkelman, B. P. Uberuaga, H. Jonsson, A climbing image nudged elastic band method for finding saddle points and minimum energy paths, The Journal of chemical physics 113 (2000) 9901–9904.